| Admissions | Accreditation | Booksellers | Catalog | Colleges | Contact Us | Continents/States/Districts | Contracts | Examinations | Forms | Grants | Hostels | Honorary Doctorate degree | Instructors | Lecture | Librarians | Membership | Professional Examinations | Programs | Recommendations | Research Grants | Researchers | Students login | Schools | Search | Seminar | Study Center/Centre | Thesis | Universities | Work counseling |
|
What is Trigonometry? What can you do with trig? Why is trigonometry important? How is it used in the real world? What are the etymologies of the six trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent? How do I find sines and cosines without using a calculator? What is Trigonometry? In modern mathematics, there are six main trigonometric functions, also called trigonometric formulas: sine, tangent, secant, cosine, cotangent, and cosecant. These functions describe the ratios of the sides of right triangles. Trigonometric identities include Pythagorean identities, reduction formulas, and cofunction identities. Often, a trigonometry calculator is used to solve trig problems. Trigonometry courses may cover study topics such as how to use the trigonometric functions to solve right triangles, and the Pythagorean Theorem. In addition, non-right angled triangles can be solved using the sine and cosine trigonometric functions. More advanced educational courses may include the study of complex numbers, polar coordinates, De Moivre's Theorem, and Euler's Formula. Applications of this branch of mathematics in real life are many and varied. Engineers in many industrial fields use trig in the course of their work. Other professionals that may use trigonometry include surveyors, astronomers, architects, and pilots. A common real life problem that may be solved using the rules of trigonometry is to work out the measurements of things or spaces that would be difficult to measure directly in a traditional way. For example, trigonometric functions can be used to work out the heights of mountains, the quantity of water in a lake, or the square footage of a piece of land that is an unusual shape. Trigonometry can even be used to help astronomers measure time accurately. What can you do with trig? Historically, it was developed for astronomy and geography, but scientists have been using it for centuries for other purposes, too. Besides other fields of mathematics, trig is used in physics, engineering, and chemistry. Within mathematics, trig is used in primarily in calculus (which is perhaps its greatest application), linear algebra, and statistics. Since these fields are used throughout the natural and social sciences, trig is a very useful subject to know. model of the solar system. Why is trigonometry important? One day a few of the brighter scientists and mathematicians started noticing a relationship between trigonometric concepts, such as sine and cosine, and the algebraic concept of a function. It was soon realized that the sine, cosine, and tangent could all be represented as a function, thus cementing the ties between algebra and trigonometry forever. The reason why trigonometry is so important lies all around us every day, although most of us are blissfully unaware of what trigonometry does for us in our lives. It would not be possible to build a car without trigonometry. The homes we live in are built using trigonometry. Just about every piece of technology we take for granted is researched, developed, and manufactured based on some trigonometric knowledge somewhere along the line. Navigation and surveying are also heavily dependent on trigonometry. Without it, we would never have been able to send men to the moon since we need trigonometry to compute launch trajectories, orbital trajectories, and reentry trajectories. Thanks to our knowledge of trigonometry, we can build concert halls filled with the incredibly rich and complex sounds of a symphony orchestra. Much of our knowledge about waves (sound, light, water, etc…) comes from trigonometry. So, is trigonometry important? Definitely a resounding YES! Learn it, know it, use it to enhance your life. Theoretically, you could go through life completely ignorant of what trigonometry is capable of doing for you. You could have no knowledge of trigonometry, or any mathematics. Many people do. The drawback to such a life is that one is then not able to understand the wonders that nature has to offer. Mathematics is the tool by which we, as human beings, are able to understand the unfathomable beauty of the universe. The primary application of trigonometry is found in scientific studies where precise distances need to be measured. The techniques in trigonometry are used for finding relevance in navigation particularly satellite systems and astronomy, naval and aviation industries, oceanography, land surveying, and in cartography (creation of maps). Now those are the scientific applications of the concepts in trigonometry, but most of the math we study would seem (on the surface) to have little real-life application. So is trigonometry really relevant in your day to day activities? You bet it is. Let's explore areas where this science finds use in our daily activities and how we can use this to resolve problems we might encounter. Although it is unlikely that one will ever need to directly apply a trigonometric function in solving a practical issue, the fundamental background of the science finds usage in an area which is passion for many - music! As you may be aware sound travels in waves and this pattern though not as regular as a sine or cosine function, is still useful in developing computer music. A computer cannot obviously listen to and comprehend music as we do, so computers represent it mathematically by its constituent sound waves. And this means that sound engineers and technologists who research advances in computer music and even hi-tech music composers have to relate to the basic laws of trigonometry. Trigonometry Worksheets Trigonometry Worksheets Listed Alphabetically: 1. Absolute Value 2. Absolute Value Equations 3. Absolute Value Equations 4. Absolute Value Inequalities 5. Absolute Value Inequalities 6. Absolute Value of Complex Numbers 7. Absolute Value of Complex Numbers 8. Adding and Subtracting Complex Numbers 9. Adding and Subtracting Rational (Fractional) Expressions 10. Angle Sum and Difference, Double Angle and Half Angle Formulas 11. Arc Length and Radian Measure 12. Area of Triangle Using Trigonometry 13. Arithmetic and Geometric Sequences and Series 14. Binomial Probability 15. Central Tendency and Dispersion 16. CoFunctions 17. Comparison of Volumes of Similar Solids 18. Completing the Square 19. Composition of Functions 20. Cosine: Find the value of x 21. Direct and Inverse Variation 22. Direct Variation 23. Division of Rational (Fractional) Expressions 24. Equations of Circles 25. Evaluating Rational (Fractional) Exponents 26. Exponential Expressions and Equations 27. Exponential Functions 28. Factoring Polynomials 29. Fill in the missing angle 30. Functions - Domain and One-to-one, Onto 31. Functions - Recognize and Evaluate 32. Graphically Represent the Inverse of a Function 33. Graphing Complex Numbers 34. Graphs Dealing with Sine and Cosine 35. Graphs Dealing with Tangent, Cotangent, Secant, Cosecant 36. Graphs of Circles 37. Graphs of Polynomial Equations of Higher Degree 38. Imaginary Unit and Standard Complex Form 39. Inverse Functions 40. Inverse Trigonometry Functions 41. Law of Cosines 42. Law of Sines 43. Law of Sines and the Ambiguous Case 44. Length of a Line Segment - Distance 45. Linear - Quadratic Systems 46. Logarithmic Equations 47. Logarithmic Expressions 48. Logarithmic Functions 49. Multiplying and Dividing Complex Numbers 50. Multiplying and Dividing Complex Numbers 51. Multiplying Rational (Fractional) Expressions 52. Nature of Roots - Sum and Product 53. Normal Distribution and Standard Deviation 54. Permutations and Combinations 55. Polynomial Equations of Higher Degree 56. Positive, Negative and Zero Exponents 57. Powers of i 58. Proportions 59. Pythagorean Identities 60. Quadratic Inequalities 61. Radical Equations 62. Radicals 63. Rational (Fractional) Exponents 64. Rational Equations 65. Rational Inequalities 66. Rationalizing Denominators with Radicals 67. Recursive Sequences 68. Reference Angles and Triangles 69. Regression Analysis 70. Scale Drawing 71. Sequences 72. Sigma Notation and Series 73. Similar Polygons: Ratio of Perimeters & Areas 74. Simplifying Complex Fractions/Expressions 75. Simplifying Rational (Fractional) Expressions 76. Simplifying Square Roots with Negative Numbers 77. Solving Combinations of Variations 78. Solving Quadratic Equations 79. Solving Quadratic Equations with Complex Roots 80. Special Right Triangles (Geometry emphasis) 81. Special Right Triangles (Trigonometry emphasis) 82. The Binomial Theorem 83. The Discriminant 84. Theoretical and Empirical Probabilities 85. Transformations with Functions 86. Trigonometric Equations 87. Trigonometric Functions 88. Trigonometric Ratios 89. Trigonometric Word Problems 90. Working with Right Triangles Trigonometry is usually taught in middle and secondary schools either as a separate course or as part of a precalculus curriculum. It has applications in both pure mathematics and applied mathematics, where it is essential in many branches of science and technology. A branch of trigonometry, called spherical trigonometry, studies triangles on spheres, and is important in astronomy and navigation. There are an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves. Fields that use trigonometry or trigonometric functions include astronomy (especially for locating apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development. Sine - Cosine - Tangent Very Basic Trignometry 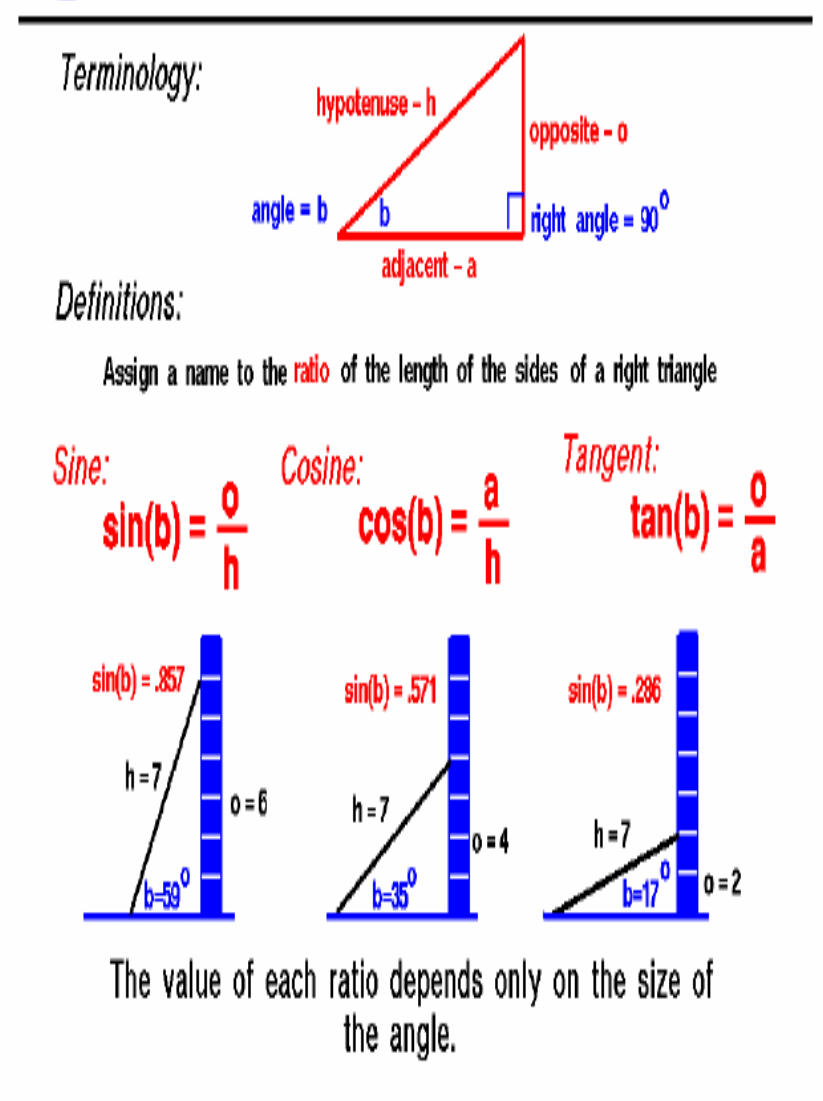 We start with a right triangle. A right triangle is a three sided figure with one angle equal to 90 degrees. (A 90 degree angle is called a right angle.) We define the side of the triangle opposite from the right angle to be the hypotenuse, "h". It is the longest side of the three sides of the right triangle. The word "hypotenuse" comes from two Greek words meaning "to stretch", since this is the longest side. We pick one of the other two angles and label it b. We don't have to worry about the other angle because the sum of the angles of a triangle is equal to 180 degrees. If we know one angle is 90 degrees, and we know the value of b, we then know that the value of the other angle is 90 - b. There is a side opposite the angle "b" which we designate o for "opposite". The remaining side we label a for "adjacent", since there are two sides of the triangle which form the angle "b". One is "h" the hypotenuse, and the other is "a" the adjacent. So the three sides of our triangle are "o", "a" and "h", with "a" and "h" forming the angle "b". We are interested in the relations between the sides and the angles of our right triangle. While the length of any one side of a right triangle is completely arbitrary, the ratio of the sides of a right triangle all depend only on the value of the angle "b". We illustrate this fact at the bottom of this page. Let us first define the ratio of the opposite side to the hypotenuse to be the sine of the angle "b" and give it the symbol sin(b). sin(b) = o / h The ratio of the adjacent side to the hypotenuse is called the cosine of the angle "b" and given the symbol cos(b). It is called "cosine" because its value is the same as the sine of the other angle in the triangle which is not the right angle. cos(b) = a / h Finally, the ratio of the opposite side to the adjacent side is called the tangent of the angle "b" is given the symbol tan(b). tan(b) = o / a To demonstrate that the value of the sine, cosine and tangent depends on the angle "b", let's study the three examples at the bottom of the figure. We are only going to discuss the sin(b) in these examples, but there are similar discussions for the cosine and tangent. In the first example, we have a 7 foot ladder that we lean against a wall. The wall is 7 feet high, and we have drawn white lines on the wall at one foot intervals. The length of the ladder is fixed. If we incline the ladder so that it touches the 6 foot line, the ladder forms an angle of nearly 59 degrees with the ground. The ladder, ground, and wall form a right triangle. The ratio of the height on the wall (o - opposite), to the length of the ladder (h - hypotenuse), is 6/7, which equals roughly .857. This ratio is defined to be the sine of b = 59 degrees. (On another page we show that if the ladder is twice as long (14 feet), and is inclined at the same angle(59 degrees), that it reaches twice as high (12 feet). The ratio stays the same for any right triangle with a 59 degree angle.) In the second example, we incline the 7 foot ladder so that it only reaches the 4 foot line. As shown on the figure, the ladder is now inclined at a lower angle than in the first example. The angle is about 35 degrees, and the ratio of the opposite to the hypotenuse is now 4/7, which equals roughly .571. Decreasing the angle decreases the sine of the angle. In example three, we incline the 7 foot ladder so that it only reaches the 2 foot line, the angle decreases to about 17 degrees and the ratio is 2/7, which is about .286. As you can see, for every angle, there is a unique point on the wall that the 7 foot ladder touches, and it is the same point every time we set the ladder to that angle. Mathematicians call this situation a function. Since the sine, cosine, and tangent are all functions of the angle "b", we can determine (measure) the ratios once and produce tables of the values of the sine, cosine, and tangent for various values of "b". Later, if we know the value of an angle in a right triangle, the tables tells us the ratio of the sides of the triangle. If we know the length of any one side, we can solve for the length of the other sides. Or if we know the ratio of any two sides of a right triangle, we can find the value of the angle between the sides. We can use the tables to solve problems. Some examples of problems involving triangles and angles include the descent of a glider, the torque on a hinge, the operation of the Wright brothers' lift and drag balances, and determining the lift to drag ratio for an aircraft. Here are tables of the sine, cosine, and tangent which you can use to solve problems. Table of sin(a) Table of cos(a) Table of tan(a) 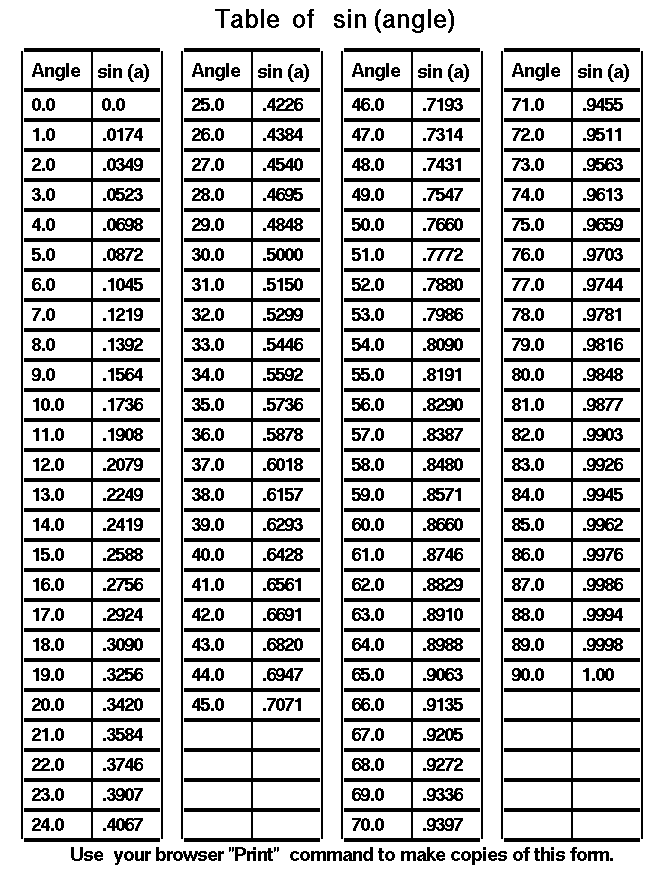 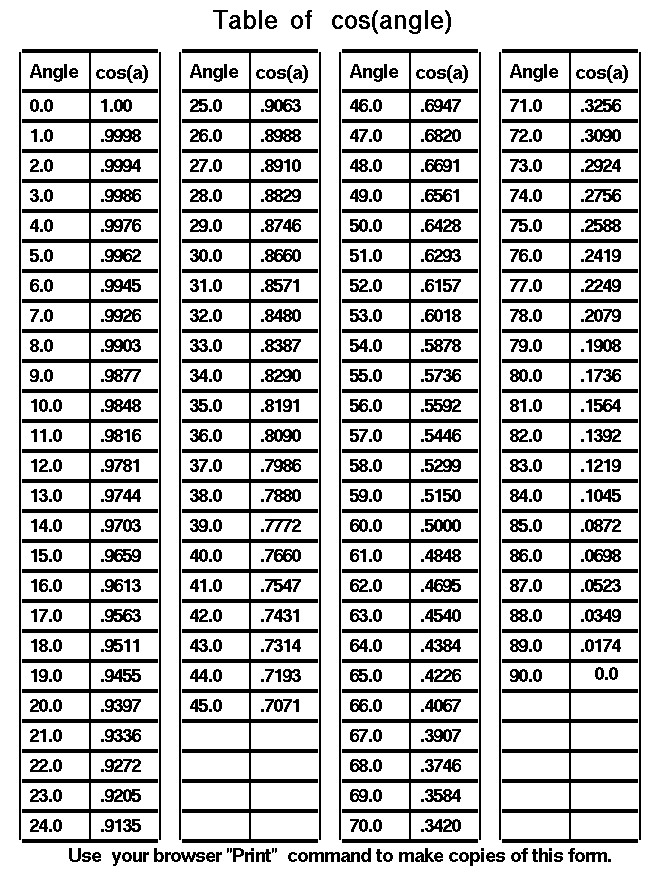 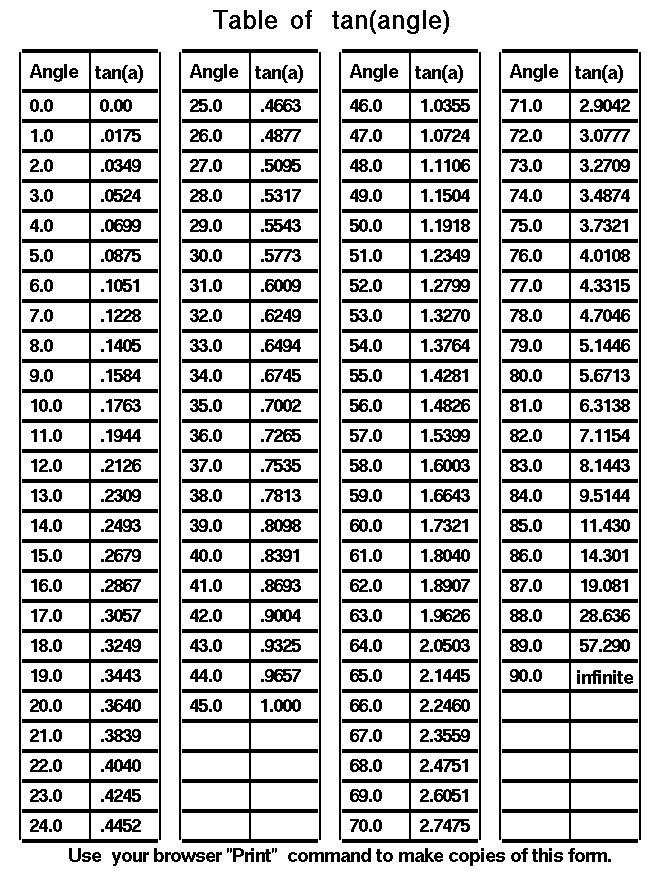  To better understand certain problems involving aircraft and propulsion it is necessary to use some mathematical ideas from trigonometry, the study of triangles. Most people are introduced to trigonometry in high school. There are many complex parts to trigonometry, but on this page we are concerned chiefly with definitions and terminology. We start with a general triangle. A triangle is a closed shape having three sides and three internal angles. The sum of the three angles of any triangle is 180 degrees. If we label the angles of a triangle c, d, and e, then: c + d + e = 180 degrees There are two ways to measure the angles inside a triangle. One way is to measure the angle in degrees, where 360 degrees equals a complete circle. The other way is measure the angle in radians, where 2 pi radians equals a complete circle. Therefore; 360 (degrees) = 2 * pi (radians) 1 degree = .01745 radians 1 radian = 57.2957 degrees A right triangle is a special case of the general triangle with one of its angles equal to 90 degrees. A 90 degree angle is called a right angle and that is where the right triangle gets its name. The right triangle has some special properties which are very useful for solving problems. The sum of the three angles of a right triangle is equal to 180 degrees and one of the angles equals 90 degrees. Then the sum of the other two angles is also 90 degrees. For a right triangle: c + d = 90 degrees = pi/2 radians The important factor here is that if we know (or measure) one angle of a right triangle,we automatically know the value of the other angle. If we know the value of d, then c = 90 - d To describe a triangle in general, we need to know the value of two angles; for a right triangle we only need to know (or measure) one angle. Another important piece of information relates the size of the sides of a right triangle. We call the side of the right triangle opposite from the right angle the hypotenuse. It is the longest side of the three sides of the right triangle. The word "hypotenuse" comes from two Greek words meaning "to stretch", since this is the longest side. We will label the hypotenuse with the symbol h and we will label the other two sides a and b. Regardless of the size of the hypotenuse, the ratio of the size of side a to the hypotenuse h depends only on the size of the angle between the side and the hypotenuse. The value of the ratio is a function of the angle and is given the name cosine of the angle. On the figure, cos(c) = a / h Because of the relations of the angles of a right triangle, we can define another function of the angle, called the sine of the angle, which relates side b and the hypotenuse: sin(c) = b / h The key point here is that if we measure one angle, we know the value of all three angles in a right triangle. And if we additionally measure one side, we can use these trigonometric functions to determine the length of all three sides. We can determine 5 pieces of information (2 angles and 3 sides) by making only two measurements. An additional relation exists between the sides of a right triangle. If we draw a square on the hypotenuse, and a square on each of the two sides, the area of the square on the hypotenuse is equal to the sum of the squares on the sides. This is called the Pythagorean Theorem and has been know since ancient times: h^2 = a^2 + b^2 The Pythagorean Theorem can be used with the trigonometric functions to determine the size of all the sides of a right triangle. http://www.analyzemath.com/Trigonometry.html |
